Determinan Matriks
Determinan Matriks
Salah satu bagian paling penting dari pembahasan materi matriks adalah cara menghitung determinan matriks, invers matriks, dan sifat-sifatnya. Sobat perlu meneguasai dasar cara menentukan determinan matriks, invers matriks, dan sifat-sifatnya karena akan sangat dibutuhkan untuk membantu perhitungan matriks dengan tipe soal tingkat lanjut.
Untuk pertama, sobat akan dikenalkan melalui bagian yang paling sederhana yaitu mencari determinan matriks dengan ordo 2 x 2. Untuk tingkat SMA, ulasan mengenai determinan matriks biasanya melibatkan matriks dengan ordo 2 x 2. Namun, materi determinan matriks dengan ukuran lebih besar juga sering diulas. Hanya saja tidak sesering determinan matriks ordo 2 x 2. Cara menentukan determinan matriks untuk orde lebih besar dari 3 x 3 lebih rumit dari cara menentukan determinan matriks ordo 2 x 2.
Menentukan nilai invers matriks ordo 2 x 2 cukup mudah dilakukan. Sedangkan cara menentukan invers matriks ordo 3 x 3 lebih susah dan rumit. Melalui halaman ini, sobat idschool bisa menyimak cara menentukan invers matriks dari kedua ordo tersbut.
Uraian materi yang dibahas pada halaman ini memuat apa itu determinan matriks dan bagaimana cara menentukan determinan matriks? Apa itu invers matriks dan bagaimana cara menghitung nilai invers matriks? Sifat apa saja yang dimiliki determinan matriks dan invers matriks?
Secara lebih lengkap dapat disimak pada pembahasan di bawah.
Determinan Matriks
Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau  . Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
. Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
Untuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
Determinan Matriks Ordo 2 x 2
Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
Nilai determinan A disimbolkan dengan  , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
Contoh Soal:
Tentukan nilai determinan matriks
Pembahasan:
Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.
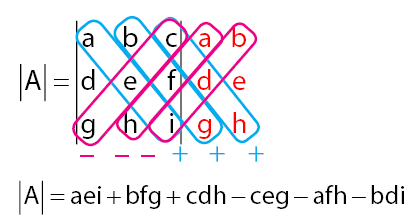
Contoh perhitungan determinan pada matriks ordo 3:
Maka,
Selanjutnya, pembahasan kita akan berlanjut ke invers matriks.
Komentar
Posting Komentar