Invers Matriks

Invers Matriks

Invers matriks dapat diartikan sebagai kebalikan dari suatu matriks tertentu. Jika suatu matriks bujur sangkar A dikalikan terhadap inversnya yaitu matriks bujur sangkar A^{-1}maka menghasilkan matriks I (matriks identitas pada operasi perkalian matriks).
Jika pada penjumlahan dua matriks, jumlah dua matriks bujur sangkar A dan -A akan menghasilkan matriks nol (matriks identitas pada operasi penjumlahan matriks).
  \[ A \cdot A^{-1} = I\]
  \[ A + (-A) = 0 \]

Invers Matriks Ordo 2 x 2
Invers dari suatu matirks A
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]
dinyatakan dalam rumus di bawah.
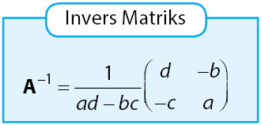
Invers Matriks
Contoh menentukan invers matriks A dapat dilihat seperti langkah-langkah berikut.
Diketahui:
  \[ \textrm{A} \; = \; \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \]
Tentukan invers dari matrik A!
Pembahasan:
  \[ \textrm{A}^{-1} \; = \; \frac{1}{3 \cdot 4 - 2 \cdot 1} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \frac{1}{12 - 2} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \frac{1}{10} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \begin{bmatrix}\frac{4}{10} & -\frac{2}{10} \\ -\frac{1}{10} & \frac{3}{10} \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \begin{bmatrix}\frac{2}{5} & -\frac{1}{5} \\ -\frac{1}{10} & \frac{3}{10} \end{bmatrix} \]

Invers Matriks Ordo 3 x 3
Cara untuk menentukan nilai invers matriks A dengan ordo 3 x 3 tidak sama dengan cara menentukan invers matriks dengan ordo 2 x 2. Cara menentukan invers matriks ordo 3 x 3 lebih rumit dari cara menentukan invers matriks 2 x 2. Melalui halaman ini, idschool akan berbagi cara menentukan invers matriks ordo 3 x 3. Simak ulasannyna pada pembahasan di bawah.
Sebelum menentukan invers matriks ordo 3 x 3, perlu dipahami terlebih dahulu mengenai matriks minor, kofaktor, dan adjoin. Simak penjelasannya pada uraian di bawah.
  1. Matriks Minor
    Diketahui sebuah matriks A dengan ordo 3 seperti terlihat di bawah.

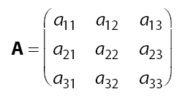    Invers Matriks Ordo 3 x 3
    Matriks minor M_{ij} adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2 seperti persamaan di bawah.

    Matriks Minor Mij
    Matriks-matriks minor di atas digunakan untuk mendapatkan matriks kofaktor A.

  2. Kofaktor
    Kofaktor baris ke-i dan kolom ke-j disimbolkan dengan C_{ij} dapat ditentukan dengan rumus seperti terlihat di bawah.
    Matriks Kofaktor
    Kofaktor di atas akan digunakan untuk menentukan adjoin matriks yang akan dicari nilai inversnya.

  3. Adjoin
    Secara umum, sebuah matriks memiliki matriks adjoin seperti ditunjukkan seperti pada matriks di bawah.
    Matriks Adjoin A
    Keterangan: C_{ij} adalah kofaktor baris ke-i dan kolom ke-j.
    Sehinnga, adjoin dari matriks A dinyatakan seperti terlihat pada persamaan di bawah \[ Adj(A) \; = \; \; \begin{bmatrix} C_{11} & C_{21} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} \]

Komentar

Posting Komentar

Postingan populer dari blog ini

Correlation Coefficient

Correlation Coefficient  A number that is a measure of the strength and direction of the correlation between two variables. Correlation coefficients are expressed using the variable r, where r is between 1 and –1, inclusive. The closer r is to 1 or –1, the less scattered the points are and the stronger the relationship. Only data points with a scatterplot which is a perfectly straight line can have r = –1 or r = 1. When r < 0 the data have a negative association, and when r > 0 the data have a positive association.
Baca selengkapnya